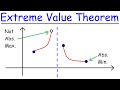
Critical Numbers and Extreme Values

The video tutorial explains the Extreme Value Theorem, which states that a continuous function on a closed interval has both a minimum and a maximum. It illustrates this with graphs, showing how to identify extrema. The video also covers Fermat's Theorem, which relates to local extrema and critical numbers, and discusses the importance of open and closed intervals in determining extrema.

What does the Extreme Value Theorem state about a continuous function on a closed interval?

• It has neither a minimum nor a maximum.

• It has both a minimum and a maximum.

• It has only a minimum.

• It has only a maximum.

In the context of the Extreme Value Theorem, what is an absolute maximum?

• A point that is not an endpoint.

• The highest point on the graph.

• A point where the derivative is zero.

• The lowest point on the graph.

What is a local maximum according to Fermat's Theorem?

• A point where the derivative does not exist.

• A point where the derivative is zero.

• A point where the derivative is negative.

• A point where the derivative is positive.

What are critical numbers in the context of Fermat's Theorem?

• Points where the derivative is zero or does not exist.

• Points where the function is not defined.

• Points where the function has a maximum value.

• Points where the function has a minimum value.

What is the role of a horizontal tangent line in identifying extrema?

• It indicates a point of inflection.

• It indicates a local maximum or minimum.

• It indicates an absolute minimum.

• It indicates an absolute maximum.

Why might a graph not have an absolute minimum?

• Because it has a local minimum.

• Because it is a closed interval.

• Because it is an open interval.

• Because it has a local maximum.

Tags

CCSS.HSF-IF.C.7D

What is the significance of open circles on a graph?

• They indicate a local minimum.

• They indicate an open interval.

• They indicate a local maximum.

• They indicate a closed interval.

In an open interval, why might a point not be considered an absolute maximum?

• Because it is a local minimum.

• Because it is not a closed circle.

• Because it is a local maximum.

• Because it is not the highest point.

What happens to the Extreme Value Theorem if the interval is not closed?

• It does not apply.

• It still applies.

• It applies only to local extrema.

• It applies only to absolute extrema.

Why is a point with an open circle not considered an absolute extremum?

• Because it is not the lowest point.

• Because it is not part of the interval.

• Because it is not a closed point.

• Because it is not the highest point.