Quadratic Equations and Triangle Theorems

The video tutorial explains how to find the value of X in a right triangle where the hypotenuse is x^4 and the other two legs are x^2 and x^3. The instructor uses the Pythagorean theorem to set up an equation and then simplifies it using exponent rules. A quadratic equation is derived and solved using the quadratic formula, leading to the discovery that X is the square root of the golden ratio, approximately 1.272. The video concludes with a call to action for viewers to subscribe.

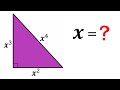
What is the hypotenuse of the right triangle in the problem?

• x^2

• x^4

• x^3

• x^5

Which theorem is used to solve for x in the triangle?

• Pythagorean theorem

• Fundamental theorem of calculus

• Fermat's Last Theorem

• Binomial theorem

What is the expression for the hypotenuse squared in terms of x?

• x^2

• x^4

• x^6

• x^8

How is x^6 rewritten using the product rule of exponents?

• x^5 * x

• x^2 * x^4

• x^3 * x^3

• x^4 * x^2

What common factor is taken out from the equation x^4 + x^4 * x^2 - x^4 * x^4?

• x^2

• x^3

• x^4

• x^5

What substitution is made to simplify the quadratic equation?

• U = x^4

• U = x^3

• U = x

• U = x^2

What is the quadratic formula used to solve for U?

• U = (-b ± √(b²-4ac)) / 2a

• U = (b ± √(b²+4ac)) / 2a

• U = (b ± √(b²-4ac)) / a

• U = (-b ± √(b²+4ac)) / a

What is the final value of x in terms of the golden ratio?

• x = (1 + √5) / 2

• x = √(1 - √5) / 2

• x = √(1 + √5) / 2

• x = (1 - √5) / 2