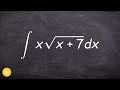
Integration Techniques and Substitution

The video tutorial explains the process of U-substitution in calculus, starting with defining u as x plus 7. It then solves for x in terms of u and demonstrates how to integrate using this substitution. The tutorial applies the power rule to integrate and simplifies the resulting expression, ensuring all steps are clear and correct.

What is the initial substitution made in the example?

• u = x - 7

• u = x + 7

• u = x/7

• u = x^2 + 7

How do we express x in terms of u?

• x = u + 7

• x = 7u

• x = u - 7

• x = u/7

What is the purpose of verifying the substitution?

• To check the limits of integration

• To solve for x

• To find the derivative of u

• To ensure the integral is set up correctly

Why can't we distribute x inside the square root?

• Because it is not mathematically valid

• Because x is already simplified

• Because it would change the integral

• Because x is not a constant

What is the result of applying the power rule to the integral?

• u to the 3 halves

• u to the 5 halves

• u to the 7 halves

• u to the 1 half

What was the sign error that needed correction?

• The positive sign was missing

• The fraction was incorrect

• The variable was incorrect

• The negative sign was added twice

What is the final step in the integration process?

• Re-evaluating the integral

• Checking the limits

• Substituting back the original variable

• Simplifying the expression

What is the final expression of the integrated function?

• 2/5 (x + 7)^(5/2) - 14/3 (x + 7)^(3/2) + C

• 3/2 (x + 7)^(5/2) - 2/5 (x + 7)^(3/2) + C

• 2/3 (x + 7)^(5/2) - 14/5 (x + 7)^(3/2) + C

• 5/2 (x + 7)^(3/2) - 3/2 (x + 7)^(5/2) + C