Area Between Curves and Integration

Professor Dave explains how to find the area between curves using integration. He starts with a conceptual understanding of subtracting areas, then provides examples with a parabola and a line, and two parabolas. The video also covers integration with respect to the y-axis.

What is the primary mathematical concept used to find the area between curves?

• Differentiation

• Integration

• Algebra

• Trigonometry

In the analogy of the square with a circular hole, what does the circle represent?

• The area to be added

• The total area

• The perimeter

• The area to be subtracted

How do we find the area between two continuous functions?

• Add their integrals

• Subtract their integrals

• Divide their integrals

• Multiply their integrals

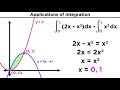
What is the first step in finding the area between the parabola x^2 + 1 and the line y = x?

• Add their integrals

• Find their intersection points

• Subtract their integrals

• Graph the functions

What is the simplified form of the integral for the area between x^2 + 1 and x?

• x^2 - x + 1

• x^2 + x + 1

• x^2 - 1

• x^2 + 1

What is the antiderivative of x^2 - x + 1?

• x^3/3 + x^2 - x

• x^3/3 + x^2/2 - x

• x^3/3 - x^2 + x

• x^3/3 - x^2/2 + x

What is the first step in solving the problem with y = x^2 and y = 2x - x^2?

• Find the area directly

• Graph the functions

• Subtract the functions

• Add the functions

What are the limits of integration for the area between y = x^2 and y = 2x - x^2?

• 0 to 1

• 0 to 2

• 0 to 3

• 0 to 4

What is the integral setup for the area between y = x^2 and y = 2x - x^2?

• 2x^2 - x

• x^2 - 2x

• x - 2x^2

• 2x - 2x^2

What technique might be needed for more complex functions?

• Multiplication

• Addition

• Division

• Substitution