What is the angle of elevation measured by the man from the ground to the top of the building?
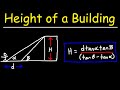
Calculating Building Heights with Angles
Interactive Video
•
Mathematics, Science
•
7th - 12th Grade
•
Hard
Aiden Montgomery
FREE Resource
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
45 degrees
60 degrees
90 degrees
30 degrees
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Which trigonometric ratio is used to calculate the height of the building in the first problem?
Sine
Cosine
Tangent
Cotangent
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
In the second problem, how far does Karen walk towards the building before measuring the new angle of elevation?
250 feet
200 feet
100 feet
150 feet
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the new angle of elevation Karen measures after walking towards the building?
45 degrees
40 degrees
35 degrees
30 degrees
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the formula for calculating the height of a building using two angles of elevation and the distance between them?
H = D / (tan Alpha - tan Beta)
H = D * tan Alpha * tan Beta / (tan Beta - tan Alpha)
H = D * (tan Alpha + tan Beta)
H = D * (tan Alpha - tan Beta)
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the height of the building calculated in the second problem?
480.86 feet
330.86 feet
277.6 feet
144.3 feet
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
Which angle should be used first in the formula to avoid a negative result?
Either angle
The larger angle
The smaller angle
Both angles
Create a free account and access millions of resources
Similar Resources on Quizizz

11 questions
Estimating the Height of a Building
Interactive video
•
9th - 12th Grade

9 questions
Trigonometric Functions and Ladder Problems
Interactive video
•
7th - 10th Grade

11 questions
Trigonometric Functions and Rocket Height
Interactive video
•
9th - 12th Grade

11 questions
Exploring Trigonometric Ratios in Right Triangles
Interactive video
•
8th - 12th Grade

11 questions
Understanding Roof Pitch and Trigonometry
Interactive video
•
7th - 12th Grade

11 questions
Solving Right Triangle Trigonometry Word Problems
Interactive video
•
6th - 10th Grade

11 questions
Tangent Function Applications in Triangles
Interactive video
•
9th - 12th Grade

11 questions
Understanding the Rate of Change of Angle of Elevation
Interactive video
•
9th - 12th Grade
Popular Resources on Quizizz

15 questions
Character Analysis
Quiz
•
4th Grade

17 questions
Chapter 12 - Doing the Right Thing
Quiz
•
9th - 12th Grade

10 questions
American Flag
Quiz
•
1st - 2nd Grade

20 questions
Reading Comprehension
Quiz
•
5th Grade

30 questions
Linear Inequalities
Quiz
•
9th - 12th Grade

20 questions
Types of Credit
Quiz
•
9th - 12th Grade

18 questions
Full S.T.E.A.M. Ahead Summer Academy Pre-Test 24-25
Quiz
•
5th Grade

14 questions
Misplaced and Dangling Modifiers
Quiz
•
6th - 8th Grade
Discover more resources for Mathematics

30 questions
Linear Inequalities
Quiz
•
9th - 12th Grade

11 questions
Decimal/fraction conversions quick check
Quiz
•
5th - 7th Grade

20 questions
Inequalities Graphing
Quiz
•
9th - 12th Grade

10 questions
Identifying equations
Quiz
•
KG - University

20 questions
Solving Linear Equations for y
Quiz
•
9th - 12th Grade

11 questions
Graph Match
Quiz
•
9th - 12th Grade

16 questions
Function or Non-Function?
Quiz
•
8th - 10th Grade

20 questions
Math Review
Quiz
•
7th Grade