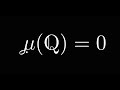
Understanding Music and Measure Theory

The video presents two challenges: one in music and another in measure theory. The first challenge explores musical harmony through frequency ratios, discussing how rational and irrational numbers affect harmony. The second challenge involves covering rational numbers between 0 and 1 with open intervals, where the sum of the intervals' lengths is less than 1. The solution involves listing rational numbers and assigning intervals, demonstrating a counterintuitive result in measure theory. The video concludes with a visual explanation, connecting the two challenges and highlighting the surprising nature of the results.

What are the two main challenges introduced in the video?

• Biology and astronomy

• Physics and chemistry

• Literature and history

• Music and measure theory

What determines whether two musical notes sound harmonious?

• The volume of the notes

• The instrument used

• The ratio of their frequencies

• The duration of the notes

Why do some rational numbers sound cacophonous?

• They have large numerators

• They have large denominators

• They are too simple

• They are too loud

What is the significance of the 12th root of 2 in music?

• It is used to determine note duration

• It is used to tune pianos

• It is used to calculate tempo

• It is used to measure volume

What is the main challenge in covering rational numbers with open intervals?

• Using only one interval

• Using intervals with a total length less than 1

• Using intervals with a total length more than 1

• Using only finite intervals

How can the sum of the lengths of intervals be less than 1?

• By using finite intervals

• By using intervals of equal length

• By using intervals with increasing lengths

• By using infinitely many intervals with decreasing lengths

What does the term 'dense' mean in the context of rational numbers?

• Rational numbers are sparse

• Rational numbers are evenly distributed

• Rational numbers are isolated

• Rational numbers are closely packed

What is the role of epsilon in the second challenge?

• It defines the starting point of intervals

• It sets the maximum length of intervals

• It determines the number of intervals

• It scales the length of intervals

How does the savant perceive musical harmony differently?

• She finds only irrational ratios harmonious

• She finds no ratios harmonious

• She finds only simple ratios harmonious

• She finds all ratios harmonious

What is the surprising connection between the two challenges?

• Both involve the concept of speed

• Both involve the concept of time

• Both involve the concept of density

• Both involve the concept of volume