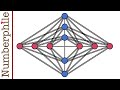
Brick Factory Problem and Graph Theory

The video discusses the brick factory problem devised by Pál Turán, focusing on minimizing track crossings in a brick-making factory. It explores simple and complex scenarios, offering solutions like arranging kilns and storage units in a circle or hexagon. A general formula for minimizing crossings is introduced, with applications in computer chip design. The video also touches on complete graphs and concludes with a promotion for Brilliant.

What inspired Pál Turán to devise the brick factory problem?

• A book he read about factory design

• A conversation with another mathematician

• His work in a forced labor camp during WWII

• His studies in university

In a simple scenario with one kiln and two storage units, what is a potential solution to avoid track crossings?

• Building a bridge over the tracks

• Adding more kilns

• Creating a loop

• Using a single straight track

What is the main challenge when connecting three kilns to three storage units?

• Finding enough space for all units

• Avoiding track crossings

• Ensuring equal distance between units

• Balancing the weight of the bricks

What is the formula used to calculate the minimum number of crossings for kilns and storage units?

• k * s

• k/2 * (k-1)/2 * s/2 * (s-1)/2

• k + s

• k^2 + s^2

What is a practical application of minimizing crossings in the brick factory problem?

• Developing new materials

• Designing efficient road networks

• Building skyscrapers

• Creating computer chips

What is a complete graph?

• A graph with only one edge

• A graph with an equal number of vertices and edges

• A graph where every point is connected to every other point

• A graph with no edges

How many crossing points does a complete graph with five dots have?

• One

• Five

• Three

• Seven

What is the significance of the formula for complete graphs?

• It helps in designing buildings

• It provides a worst-case scenario for crossings

• It is used in weather prediction

• It calculates the shortest path between points

For which values of n has the minimum number of crossings been proven?

• n less than or equal to 10

• n less than or equal to 12

• n less than or equal to 6

• n less than or equal to 15

What is the current status of the conjecture regarding the minimum number of crossings?

• It remains unproven for some values

• It has been fully proven

• It is no longer considered important

• It has been disproven