Circle OST Geometry Review Challenge

The video tutorial covers key concepts related to circles, including central and inscribed angles, the equation of a circle, and how to calculate arc length and sector area. It also explains the process of inscribing a circle within a triangle, focusing on the incenter and angle bisectors.

What is the relationship between a central angle and its intercepted arc?

• The arc is equal to the central angle

• The arc is twice the central angle

• The arc is half the central angle

• There is no relationship

Tags

CCSS.HSG.C.A.2

What is the relationship between an inscribed angle and its intercepted arc?

• The angle is equal to the arc

• The angle is twice the arc

• The angle is half the arc

• The angle is one-fourth the arc

Tags

CCSS.HSG.C.A.2

What is true about the angles in a quadrilateral inscribed in a circle?

• All angles are equal

• All angles are right angles

• Opposite angles are supplementary

• Adjacent angles are supplementary

In a quadrilateral inscribed in a circle, if one angle is 70 degrees, what is the measure of the opposite angle?

• 180 degrees

• 20 degrees

• 70 degrees

• 110 degrees

Tags

CCSS.HSG.C.A.3

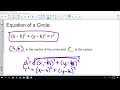
How is the equation of a circle derived using the distance formula?

• By squaring the radius and setting it equal to the sum of the squares of the differences in x and y coordinates

• By dividing the radius by the sum of the squares of the differences in x and y coordinates

• By taking the square root of the sum of the squares of the differences in x and y coordinates

• By multiplying the radius by the sum of the squares of the differences in x and y coordinates

Tags

CCSS.HSG.GPE.A.1

How do you calculate the length of an arc?

• Divide the central angle by the circumference

• Multiply the central angle by the diameter

• Multiply the central angle by the radius

• Divide the central angle by 360 and multiply by the circumference

Tags

CCSS.HSG.C.B.5

How do you find the area of a sector of a circle?

• Divide the central angle by the radius and multiply by the area of the circle

• Multiply the central angle by the area of the circle

• Divide the central angle by 360 and multiply by the area of the circle

• Multiply the central angle by the radius squared

Tags

CCSS.HSG.C.B.5

What is the formula for the circumference of a circle?

• 2 * radius / pi

• radius squared * pi

• pi * diameter

• 2 * pi * radius

Tags

CCSS.7.G.B.4

What is the role of the incenter in an inscribed circle within a triangle?

• It is the midpoint of the hypotenuse of the triangle

• It is the intersection of the triangle's altitudes

• It is the point where the angle bisectors intersect and serves as the circle's center

• It is the intersection of the triangle's medians

Tags

CCSS.HSG.C.A.3

What must be true for a circle's radius when inscribing it within a triangle?

• It must be parallel to one of the triangle's sides

• It must be perpendicular to one of the triangle's sides

• It must be equal to one of the triangle's sides

• It must bisect one of the triangle's angles

Tags

CCSS.HSG.C.A.3