What is the initial condition given for the function f in the problem?
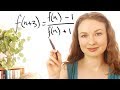
Understanding the 2003 Australian Mathematics Competition Problem
Interactive Video
•
Mathematics
•
9th - 12th Grade
•
Hard
Emma Peterson
Used 3+ times
FREE Resource
Read more
10 questions
Show all answers
1.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
f(11) = 11
f(11) = 0
f(11) = 1
f(11) = -11
2.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the formula used to find f(n+3) in terms of f(n)?
f(n+3) = f(n) - 1
f(n+3) = f(n) + 1
f(n+3) = (f(n) + 1) / (f(n) - 1)
f(n+3) = (f(n) - 1) / (f(n) + 1)
3.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the value of f(14) after applying the formula to f(11)?
1/2
11
5/6
2/3
4.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
How do you simplify the expression when dealing with fractions within a fraction?
Subtract the fractions
Divide the fractions
Add the fractions
Multiply top and bottom by the same number
5.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What is the value of f(17) after simplification?
11
-11
-1/11
1/11
6.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
What pattern is observed in the function values as n increases?
The values decrease exponentially
The values remain constant
The values form a repeating cycle
The values increase linearly
7.
MULTIPLE CHOICE QUESTION
30 sec • 1 pt
How many 3s are added to 11 to reach 2003?
664
500
1000
200
Create a free account and access millions of resources
Similar Resources on Quizizz

8 questions
GCSE Secondary Maths Age 13-17 - Algebra: Algebra - Advanced - Explained
Interactive video
•
10th - 12th Grade

11 questions
Working with Exponents and Algebraic Expressions: Simplifying and Expanding
Interactive video
•
10th - 12th Grade

8 questions
GCSE Secondary Maths Age 13-17 - Number: Fractions - Explained
Interactive video
•
10th - 12th Grade

11 questions
Understanding Linear Equations in IB Maths AI
Interactive video
•
9th - 12th Grade

11 questions
Understanding Series and Partial Sums
Interactive video
•
9th - 12th Grade

8 questions
Fractions: Solving Problems with Proportions
Interactive video
•
10th - 12th Grade

6 questions
GCSE Secondary Maths Age 13-17 - Probability & Statistics: Two Way Table - Explained
Interactive video
•
10th - 12th Grade

6 questions
GCSE Secondary Maths Age 13-17 - Algebra: Factorising 2 - Explained
Interactive video
•
10th - 12th Grade
Popular Resources on Quizizz

20 questions
math review
Quiz
•
4th Grade

20 questions
Math Review - Grade 6
Quiz
•
6th Grade

20 questions
Reading Comprehension
Quiz
•
5th Grade

20 questions
Types of Credit
Quiz
•
9th - 12th Grade

20 questions
Taxes
Quiz
•
9th - 12th Grade

10 questions
Human Body Systems and Functions
Interactive video
•
6th - 8th Grade

19 questions
Math Review
Quiz
•
3rd Grade

45 questions
7th Grade Math EOG Review
Quiz
•
7th Grade
Discover more resources for Mathematics

20 questions
EOC Math 1 Review
Quiz
•
9th Grade

20 questions
Math 1 EOC Review
Quiz
•
9th Grade

14 questions
Algebra 1 SOL Review #1
Quiz
•
9th Grade

30 questions
MATH 2 - FINAL EXAM REVIEW
Quiz
•
10th Grade

15 questions
Algebra 1 SOL Review #2
Quiz
•
9th Grade

25 questions
Active EOC Math 1 Review
Quiz
•
9th Grade

15 questions
Algebra 1 Regents Review Practice Regents
Quiz
•
9th Grade

20 questions
TSI Post Test
Quiz
•
9th - 12th Grade